An image is only a representation of the object that it is formed from. All imaging systems are imperfect: lenses suffer from manufacturing defects, an objective lens only collects a small proportion of light emanating from the specimen, and diffraction – the very means by which an image is formed – also limits image fidelity.
As the size of the object approaches the wavelength of the illuminating radiation, diffraction becomes particularly acute. Every recorded image is blurred, since the instrument used to obtain it has a finite resolving power. The process of how a lens, or objective, forms an image of any object is called convolution.
A microscope objective is often characterised by its PSF – a 2-D or 3-D description of how a single point of light (in practice a sub-resolution fluorescent bead) in the specimen is transferred into the image. The PSF of an objective lens depends upon its Numerical Aperture (NA), design, the illuminating wavelength and the contrast mode (brightfield, phase, DIC, fluorescence). A widefield PSF is shown (right).
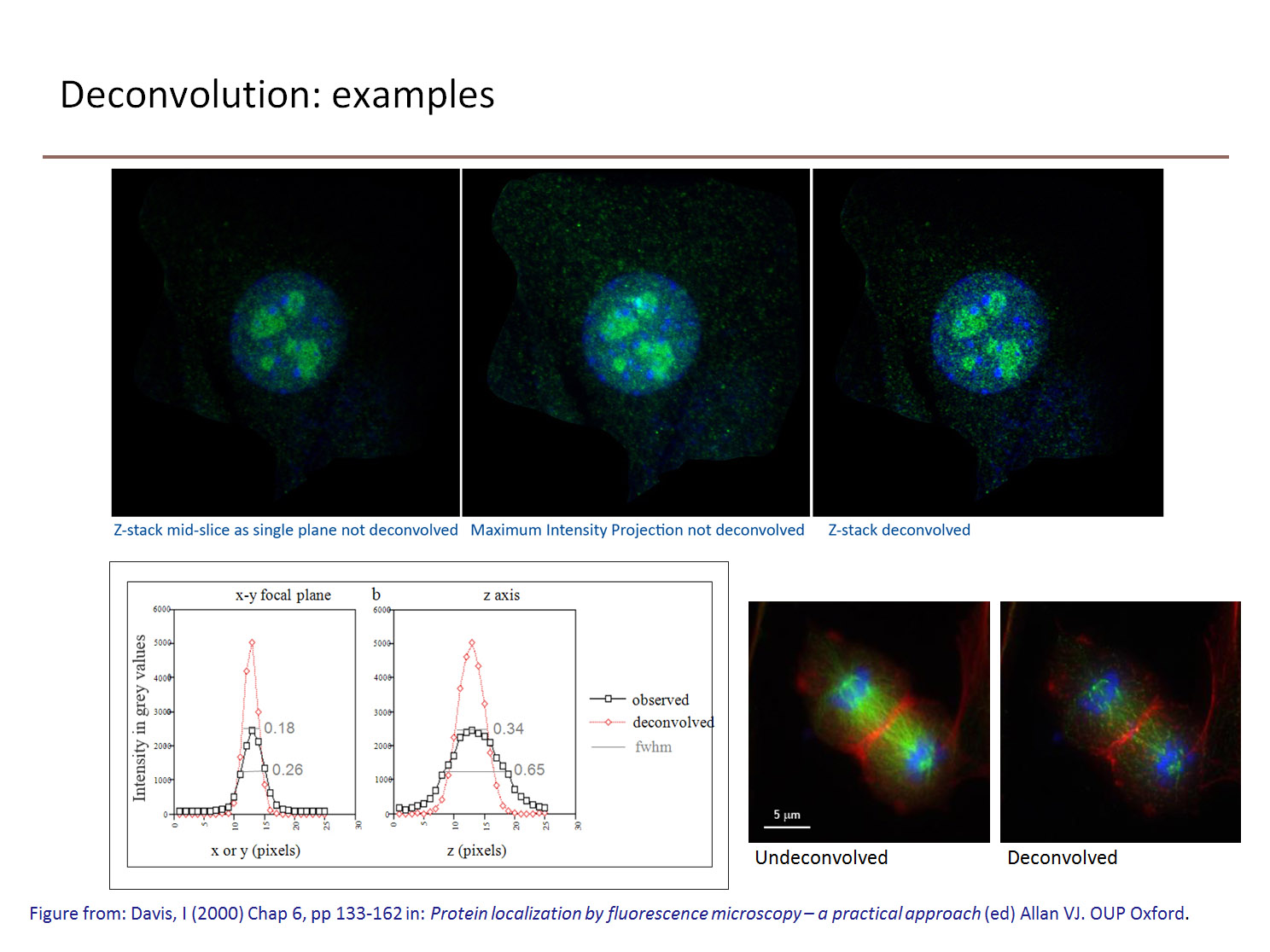
Knowing the structure and resulting image of a well-defined object (a sub-resolution fluorescent bead), the convolution process can be rigorously mathematically defined. Applying the reverse process: deconvolution, to the image allows us to ‘clean up’ the image to be a better representation of the object from which it originated.
Fluorescence images are hazy and blurred because (being self-luminous) out-of-focus information from those parts of the specimen not seen by the objective, both above and below the focal plane, spills into the focused field of view. This degrades the contrast, dynamic range and resolution of the image. If a lens behaved perfectly, and points in the object were not smeared into a point spread function (PSF), then a defocused image of beads would appear black. Deconvolution algorithms are used to reassign this out of focus light to improve the contrast in the image.
Here is a really good explanation of deconvolution by Andor. For the rest of their Microscopy School tutorials, see here.
Deconvolution microscopy (also known as computational optical microscopy) takes account of the distortion by the optical train of the microscope, and the out-of-focus signals are either:
(a) subtracted from the image or
(b) ‘reassigned’ or ‘placed back’ to the points from which they came (‘photon reassignment processing’).
While the term reassignment is consistent with the effect of their use, obviously these algorithms cannot physically replace photons to their source. However, iterative restorative deconvolution will shift and concentrate the majority of the out-of-focus fluorescence back to the focal plane of origin from which it emanated. The result of both methods (a) and (b) is an improvement in image contrast, making it easier to resolve and distinguish features in the image.
There are two main types of deconvolution algorithm: deblurring and restorative. Deblurring algorithms are nearest-neighbour based (‘digital confocal’) use an estimate of the image blurring to subtract blurred fluorescence from an image. Nearest neighbour methods use a calculated, rather than measured, PSF, and are best for thin samples. They are better suited to visualisation and volume rendering than quantitation. Images deconvolved by deblurring cannot be used for quantative measurement of intensities or calculation of ratios between fluorophores (as in calcium imaging).
Restorative methods use the PSF to ‘guess’ what the objective must have looked like. They are often iterative (changing the guess and repeating the deconvolution calculation), and use a measured or calculated PSF (derived from a sub-resolution fluorescent bead). Because the relationships between intensities is preserved using this method, quantitation is possible. The primary advantage to constrained iterative deconvolution is in boosting image contrast. Measured PSFs give increased resolution along the Z-axis. Blind deconvolution is similar to constrained iterative deconvolution, except that the PSF is not measured directly, but derived from the image data.
It is also possible to restore images acquired with a confocal or multiphoton microscope. The combination of confocal microscopy and deconvolution techniques improves resolution beyond what is generally attainable with either technique alone. Furthermore, low intensity signals contain a lot of high frequency Poisson, or shot, noise which can be erroneously sampled and digitised into non-existent single-pixel ‘features’ that could never have been resolved by the microscope. Deconvolution essentially averages the signal and removes these noise artifacts. The contrast can always be raised to match the characteristics of the display monitor. However, confocal data tends not to be deconvolved in practice because it has already been ‘sampled’ with the pinhole to produce an optical section.
References
- Microscopy primer on deconvolution
- Powerpoint on Deconvolution (pdf) Dr A Griffa, BioImaging & Optics Platform, EPFL.
- EPFL Biomedical Imaging Group pages
http://bigwww.epfl.ch/teaching/projects/abstracts/schmit/
http://bigwww.epfl.ch/algorithms/mltldeconvolution/ - Sage, D et al (2017) DeconvolutionLab2: An open-source software for deconvolution microscopy Methods 115: 28-41
- Li J-S et al (2014) Calibration of wide-field deconvolution microscopy for quantitative fluorescence imaging Jour. Biomol Tech. 25/1: 31-40
- A user’s guide (BioImaging & Optics Platform, EPFL) Part 1 & Part 2
- Goodwin, PC (2014) Quantitative deconvolution microscopy Methods Cell Biology 123: 177-192
- Biggs, DSC (2010) 3D Deconvolution Microscopy Curr. Protoc. Cytometry 12.19.1-12.19.20
- Biggs, DSC (2004) Clearing up Deconvolution. Biophotonics International, February, pp 32-37.
- Biggs, DSC (2010) A practical guide to deconvolution of fluorescence microscope imagery Microscopy Today 18/1: 10-14.
- Parton RM, Davis, I. (2006) Lifting the Fog: Image Restoration by Deconvolution Chapter 19, pp 187-200 in: Cell biology: a laboratory handbook. vol. 3, 3rd Edition. (ed) Julio E. Celis. ISBN = 978-0-12-164733-9.
- Shaw, PJ (2006) Comparison of Widefield/Deconvolution & Confocal microscopy for three-dimensional imaging Chapter 23, pp 453-467 in: Handbook of Biological Confocal Microscopy 3rd Edn. Pawley, J (ed.) Springer, New York ISBN = 987-0387-25921-5
- Conchello, J-A (2006) An overview of three-dimensional and four-dimensional microscopy by computational deconvolution, Chapter 9, pp 177-199 in: Cell Imaging. (ed) David Stephens. ISBN = 978-1-90-484204-0.
- Wallace W, Schaefer LH, Swedlow JR (2001) A Workingperson’s guide to Deconvolution in Light Microscopy. Biotechniques 31 (5): 1076-1097.
- McNally JG, Karpova T, Cooper J, Conchello J-A. (1999) Three-dimensional imaging by deconvolution microscopy. Methods 19/3: 373-85
- Sarder, P & Nehorai, A (2006) Deconvolution methods for 3-D fluorescence microscopy images IEEE Signal Processing magazine, May 2006
- Hiraoka, Y; Sedat, JW & Agard, DA (1990) Determination of three-dimensional imaging properties of a light microscope system: partial confocal behavior in epifluorescence microscopy Biophys. Jour. 57/2: 325-333 – the original paper that introduced deconvolution to microscopy